


Chapter 2 Getting StartedWhile the full details of WHIZARD’s capabilities are explained in the later chapters, a simple working example should give some flavor of the program. 2.1 Evaluating a total cross sectionFirst of all, WHIZARD has to be installed on your computer. It is designed to run on UNIX systems and has been successfully tested on several Linux OS as well as MAC OS X. While many features it uses are standard nowadays (see Sec.3), some are not, and you should check first:
WHIZARD has been extensively tested only on Linux PC and Alpha (DEC/Compaq) systems; feedback for other platforms is welcome. When these conditions are met, you should switch to an empty
directory, e.g. cd whizard Next, the package has to be configured: ./configure Inspect the output of configure and look for warnings and errors. It may happen that some environment variables have to be set so that the configure script can find all it is looking for (see Sec. 3.3.2). (Except for very old systems, WHIZARD compiles with the system Fortran 95 compiler, and on most operating system, O’Caml is also available as a package.) After configuration, you have to choose the physics model and the
processes you are interested in. You are free to specify an arbitrary
list of scattering processes, which you write into the configuration
file After this is done, the compilation procedure (see below) results in
an executable named To be specific, let us consider W pair production with a four-fermion final state:
The corresponding configuration file # The selected model model SM # Processes # Tag In Out Method Option #===================================================== cc10 e1,E1 e2,N2,u,D omega
The lines beginning with The keyword Next, the following command makes the executable and installs it in
the subdirectory named make prg install This runs fully automatically, but it will take some time: The O’Mega matrix element generator has to be compiled, then the process matrix element has to be constructed as a Fortran program and compiled, auxiliary programs have to be compiled as well, and so on. Finally, everything is linked into the single program named whizard. The subdirectory The cd results
and edit the input file &process_input process_id = "cc10" sqrts = 500 / &integration_input / &simulation_input / &diagnostics_input / ¶meter_input Mmu = 0 / &beam_input / &beam_input / When this is done, we can start the program: ./whizard On screen, WHIZARD will first display a header ! WHIZARD 1.97 (May 31 2011) ! Reading process data from file whizard.in ! Wrote whizard.out ! ! Process cc10: ! e a-e -> mu a-nu_mu u a-d ! 32 16 -> 1 2 4 8
This states that, at the very beginning, an output file
There follow several informational lines which you may ignore since the program takes care of all necessary steps by itself. Nevertheless, some explanation might be in order: Before starting integration, WHIZARD constructs a phase-space setup. The program uses an adaptive multi-channel integration method. This involves the simultaneous use of multiple phase-space parameterizations (channels), which roughly correspond to dominant Feynman diagrams of the selected process. (Note that the absence of a channel only means that it is not taken into account for a specific phase space mapping, but the corresponding Feynman diagrams are nevertheless contained in the evaluated O’Mega amplitude.) Therefore, the physics model is taken into account: ! Reading vertices from file whizard.mdl ... ! Model file: 54 trilinear vertices found. ! Model file: 54 vertices usable for phase space setup.
The model file ! Generating phase space channels for process cc10... ! Phase space: 8 phase space channels generated. ! Scanning phase space channels for equivalences ... ! Phase space: 8 equivalence relations found. ! Note: This cross section may be infinite without cuts. ! Wrote default cut configuration file whizard.cc10.cut0 ! Wrote phase space configurations to file whizard.phx
The resulting set of channels is written to a file The weights of the channels will be adapted iteratively. Furthermore, each integration dimension is binned, and the location of bins (the grid) will also be iteratively adapted for each channel. In the present case, this amounts to ! Created grids: 8 channels, 8 dimensions with 20 bins After these preliminaries, the program starts integration. It chooses 20,000 calls for each iteration of the adaptive iteration procedure, which takes some time to evaluate. Finally, the output looks like this:
At the beginning of each integration pass, the kinematical cuts are
read, which are either specified by the user in a cut definition file
or, if this information is absent as in the present case, the default
set of cuts is used. (The letter The next lines allow the user to follow the convergence of the integral during the adaptation procedure. For each iteration, the display shows the iteration index, the number of phase space points sampled, the total cross section estimate, and the error estimate: the absolute value, the relative percentage, and the relative error multiplied by the square root of the number of calls. The latter number should be of order one; in our example it is slightly below one in the final iterations. During this procedure, the currently best result is always marked by an asterisk. Note that each integral estimate is independent of each other; no accumulated integrals are shown. In some iterations the accuracy apparently does not improve, but after 12 iterations the grid and weight adaptation has nevertheless reduced the error estimate for a single sample by a factor 5. The last column shows an estimate for the reweighting efficiency when generating actual Monte-Carlo events. Since we have not yet enabled event generation, it is for informational purpose only. Note that this number tends to be less stable than the integration error, but adapting the grids has nevertheless considerably improved this value. The final result in the last row is evaluated by averaging three further iterations of 20,000 events each. The preceding results are discarded since (at early stages of the adaptation) they may be systematically off the correct result. The total cross section is thus estimated as
There is also a χ2 value given which results from comparing the three independent samplings which make up the final integration step. If this value is much larger than 1, we should mistrust the error estimate. Here, the value 0.26 indicates a well-behaved result. There are a few more lines in the output: ! ! Time estimate for generating 10000 unweighted events: 0h 00m 04s !============================================================================= ! Summary (all processes): !----------------------------------------------------------------------------- ! Process ID Integral[fb] Error[fb] Err[%] Frac[%] !----------------------------------------------------------------------------- cc10 2.7082438E+02 7.23E-01 0.27 100.00 !----------------------------------------------------------------------------- sum 2.7082438E+02 7.23E-01 0.27 100.00 !============================================================================= ! Wrote whizard.out ! Integration complete. ! No event generation requested
The time estimate for event generation (see below) may be taken as a
rough guideline, based on the previous reweighting efficiency
estimate. Then, the result is repeated – if we had selected more
than one process for integration, the individual cross sections would
be summarized here. Finally, we get reminded that the input and
output data have been saved in the file 2.2 Generating eventsThe results we have obtained can be used for event generation. Apart from the total cross section which is displayed on screen, the adaptive integration procedure produces a set of sampling grids, tailored to the given process and parameter set, which are written on disk and allow the generation of true Monte-Carlo events. To this end, we restart the program (of course, we could have done it
in a single step). We do not like to repeat the lengthy adaptation
procedure, therefore we tell WHIZARD to reuse the grids.
Furthermore, we specify a certain luminosity, say, 10 fb−1.
The modified input file &process_input process_id = "cc10" sqrts = 500 luminosity = 10 / &integration_input read_grids = T / &simulation_input / &diagnostics_input / ¶meter_input Mmu = 0 / &beam_input / &beam_input / The output looks as before (recall that the results are now read from file), but after displaying the integral the program continues and generates the appropriate number of Monte-Carlo events: ! Reading analysis configuration data from file whizard.cut5 ! No analysis data found for process cc10 ! Event sample corresponds to luminosity [fb-1] = 9.999 ! Event sample corresponds to 22344 weighted events ! Generating 2708 unweighted events ... When this is finished, the program displays a summary: ! Event generation finished. !============================================================================= ! Analysis results for process cc10: ! It Events Integral[fb] Error[fb] Err[%] Acc Eff[%] Chi2 N[It] !----------------------------------------------------------------------------- 13 2708 2.7082438E+02 5.20E+00 1.92 1.00 100.00 !----------------------------------------------------------------------------- ! Warning: Excess events: 5.1 ( 0.19% ) | Maximal weight: 1.95 The integral is unchanged (by definition), but the given error is now the statistical error which corresponds to the size of the event sample (2708 events). The 100 % efficiency just tells us that there were no additional cuts in the event generation pass; if there were some, it would be the percentage of events that passed the cuts. The excess events (the sum of all weights exceeding 1) are few enough that they can be safely ignored. Actually, the largest event weight was 1.95 which tells us that the reweighting efficiency estimate – the ratio of the average and the highest weight – has been slightly too optimistic. (In a Monte-Carlo approach of this complexity, it is impossible to calculate the highest possible event weight; it can only be approximated, and there is always a chance for fluctuations.) 2.3 Analyzing eventsClearly, such a run is not very useful without doing anything with the generated events. Fortunately, they have been written to file (in a compressed machine-dependent format) and can be reread in a subsequent run (again, we could also have done it in a single run). We might like to investigate the distributions of the hadronic
invariant mass near the W pole and of the muon energy in our event
sample. To achieve this, we set up a file named # Analysis configuration file for the process ee -> mu nu u d process cc10 histogram M of 12 within 70 90 nbin 20 and histogram E of 1 within 0 500 nbin 25 Again, the binary codes of the particles come into play. Recall that they are in the present example
The muon is thus assigned the number 1, and the combination ud is assigned the number 12=4+8. We have still to tell the program to reuse the previous event sample. In the input file, we change the block &simulation_input / to &simulation_input read_events = T / and restart the program. In the output, the program now says ! Found 2 analysis configuration datasets
and shows two identical summaries, one for each dataset. However, it
has also generated the required distributions. Those are in the file
!============================================================================= ! WHIZARD 1.97 (May 31 2011) ! Process cc10: ! e a-e -> mu a-nu_mu u a-d ! 32 16 -> 1 2 4 8 ! Analysis results for process cc10: ! ! Histograms: ! histogram M of 12 within 7.00000E+01 9.00000E+01 nbin 20 70.5000000 5.00000000 2.23606798 0.00000000 71.5000000 13.0000000 3.60555128 0.00000000 72.5000000 10.0000000 3.16227766 0.00000000 73.5000000 17.0000000 4.12310563 0.00000000 ... The first column shows the bin midpoints, the second column the number of events, and the third column the statistical error √nevt. The fourth column shows excess events if there are any. The contents of this file can be displayed graphically by standard analysis packages. For convenience, WHIZARD is able to do this by itself, using a macro package for the MetaPost drawing program4. The simple command 5 make plots
will execute all necessary steps automatically. The result is a
PostScript file called 2.4 Further optionsThe above example covers only basic features of WHIZARD. Some further possibilities, which are explained in the subsequent chapters of this manual, are:



|
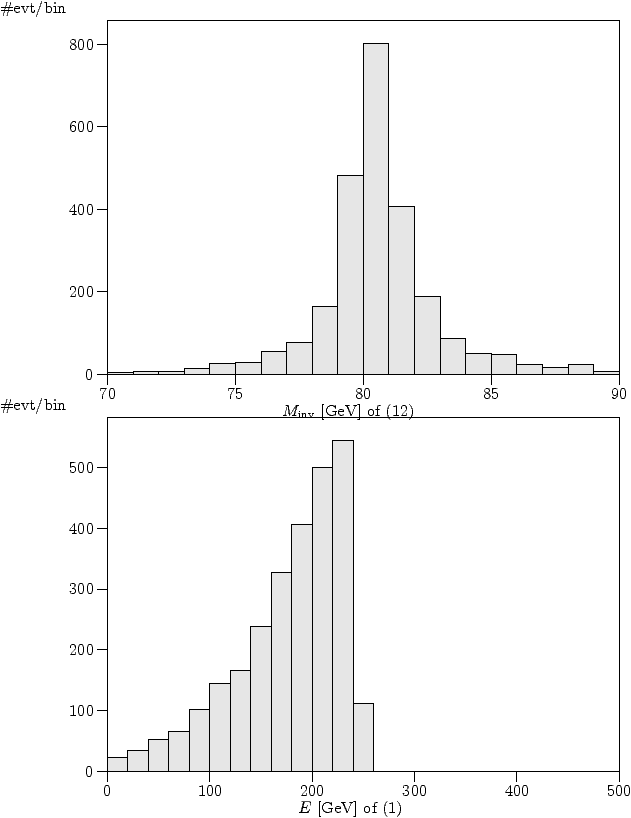 As expected, the hadronic invariant mass concentrates around the W
mass, while the muon energy shows a smooth distribution.
As expected, the hadronic invariant mass concentrates around the W
mass, while the muon energy shows a smooth distribution.